来不及解释了,先上车(Letter Combinations of a Phone Number)看题。
嫌打开链接慢的接着往下看,我把题目搬出来了。
Letter Combinations of a Phone Number
Given a digit string, return all possible letter combinations that the number could represent.A mapping of digit to letters (just like on the telephone buttons) is given below.
Input:Digit string “23”
Output: [“ad”, “ae”, “af”, “bd”, “be”, “bf”, “cd”, “ce”, “cf”].
我打开题目的标签一看,上面显示Backtracing(回溯),意思是这道题可以用回溯算法来解,那我们先了解一下回溯算法。
回溯算法
回溯算法实际上就是一种搜索算法,它跟穷举算法很相似,但是它比穷举要聪明,它会利用一些条件规避掉一些无用解。回溯算法主要分为4个步骤:
1.抽象出问题的解空间,为了便于理解,可以将解空间抽象成一颗树的结构
2.采用DFS(深度优先)算法遍历所有的解空间
3.利用限制条件(分析得出)过滤掉一些无用解,即不用对无用解进行遍历
4.输出所有解
针对leetcode的这道题目,实际上就是列出所有解,并不需要规避掉无用解。我们开始会想到用常规的for循环嵌套去解决,比如输入“23”,我们可以先循环abc再循环def进行组合输出。但是比较麻烦的是输入内容不是固定的,你不知道for循环有几层,这个是动态的,当然不排除某些大神可以想到别的方法遍历输出。
我们尝试下用回溯算法解这道题,按照步骤
1.我们先找到问题的解空间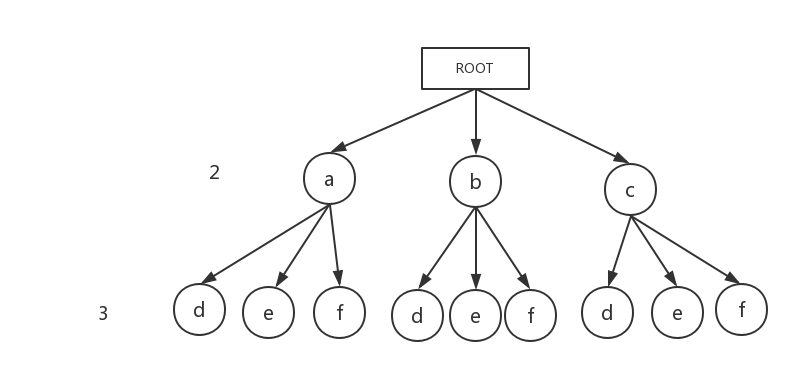
我们以一个树的结构来表示解空间,实际上这道题我们的解可以理解成为是一个路径,例如a->d,只不过我们最后输出的结果是以ad这种格式输出,所以我们可以将每个解称为解向量,解空间就是包含所有的解向量的一个整体。
如图,我们每个解从ROOT结点出发,这个点我们定义的起点,不会包含在解向量中。
2.按照DFS遍历解空间
我们选择2键盘对应的abc 3个字母中的一个,我们选择了a,3键盘在2键盘后面按下的,那么我们认为3键盘包含的所有字母为2键盘中每个字母的子结点。我们选择其中一个子结点d,此时我们已经遍历到最深处了,我们可以输出此时的解ab。然后我们回溯到上一个结点a,接着去选择它没有遍历过的子结点e,以此类推。DFS过程也可以参照下图来理解: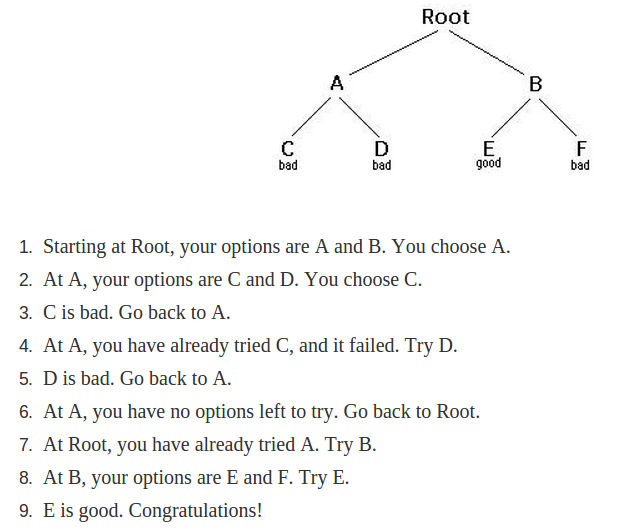
3.利用限制条件过滤掉无用解
这道题实际上没有限制条件,当然我们也可以认为以下情况为限制条件,就是从d回溯到a,将d结点标示成已经访问,然后a重新选择子节点时过滤掉已经访问的d结点,当a结点遍历完所有的d,e,f结点后回溯到ROOT结点时将d,e,f重置为未访问。
4.输出所有解
在我们步骤3的时候找出满足条件的解就可以直接输出了,例如ad,ae等,或者将每个解保存在一个全局变量中,最后进行输出。
编码
我认为回溯算法逻辑上比较复杂的地方在与抽象出解空间,如果你抽象不出来问题的解空间,那么你就没法往下进行求解了。
而编码部分较麻烦部分在于DFS遍历,我们可以使用递归或者利用栈来实现DFS。DFS一个递归实现的伪代码如下,true和false可以理解为是否为该题的一个解:
boolean solve(Node n) {
if n is a leaf node {
if the leaf is a goal node, return true
else return false
} else {
for each child c of n {
if solve(c) succeeds, return true
}
return false
}
}
而过滤无用解(俗称剪枝函数)的构建将决定你回溯算法的快慢和最后得出的解是否正确,假设解空间遍历需要循环嵌套1000次,你在第一次循环时就判断出来后面的循环得出的解都是无用解,此时你直接回溯到上级结点,不要等到你循环到底在去判断是否正确,这样时间复杂度会降低很多。
实现代码如下:
public class LetterCombinations {
private static final Map<Character, String> map = new HashMap<>();
private static final List<String> result = new ArrayList<>();
static {
map.put('2', "abc");
map.put('3', "def");
map.put('4', "ghi");
map.put('5', "jkl");
map.put('6', "mno");
map.put('7', "pqrs");
map.put('8', "tuv");
map.put('9', "wxyz");
}
/**
* Input:Digit string "23"
* Output: ["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].
*/
public static void main(String[] args) {
LetterCombinations letterCombinations = new LetterCombinations();
letterCombinations.letterCombinations("237");
System.out.println(result);
}
public void dfs(String digits, String s) {
if (digits.length() == 1) {
String str = map.get(digits.charAt(0));
for (int i = 0; i < str.length(); i++) {
result.add(s + str.charAt(i));
}
} else {
Character lastChar = digits.charAt(0);
String relatedStr = map.get(lastChar);
for (int i = 0; i < relatedStr.length(); i++) {
Character tempChar = relatedStr.charAt(i);
dfs(digits.substring(1), s + tempChar);
}
}
}
public List<String> letterCombinations(String digits) {
if (digits == null || digits.equals("")) {
return Collections.emptyList();
}
dfs(digits, "");
return result;
}
}
主要递归实现思想,我们要求237的所有结果,我们可以先递归求37的所有结果,我们求37的结果可以先看7的所有解,每次递归求解时将当前选择的字母(即上图中所说的结点)带过去,最后将解放到集合中。
这题的过滤无用解没有体现出来,感兴趣的可以看看下面这个素数环题目,这题比上面要难一些。
/**
* Created by linuxv on 17-3-21.
* see http://acm.hdu.edu.cn/showproblem.php?pid=1016
* A ring is compose of n circles as shown in diagram. Put natural number 1, 2, ..., n into each circle separately, and the sum of numbers in two adjacent circles should be a prime.
* Note: the number of first circle should always be 1.
* <p/>
* n (0 < n < 20).
*/
public class PrimeCircle {
private static final int N = 20;
//记录是否是素数
private static final boolean[] isPrimeArr = new boolean[N + 1];
//记录是否遍历过
private static final boolean[] isVisit = new boolean[N + 1];
private static final int[] result = new int[N + 1];
static {
//先将1-20以内的所有素数和和数区分开,用数组下标表示数,对于数组值为true表示是素数,false表示不是素数
for (int i = 1; i <= N; i++) {
boolean isPrime = true;
for (int j = 2; j * j <= i; j++) {
if (i % j == 0) {
isPrime = false;
break;
}
}
isPrimeArr[i] = isPrime;
}
}
public static void dfs(int index, int n) {
if (index == n && isPrimeArr[result[0] + result[n - 1]]) {
for (int i = 0; i < n - 1; i++) {
System.out.print(result[i] + "-");
}
System.out.println(result[n - 1]);
} else {
for (int i = 2; i <= n; i++) {
if (!isVisit[i] && isPrimeArr[result[index - 1] + i]) {
result[index] = i;
isVisit[i] = true;
dfs(index + 1, n);
isVisit[i] = false;
}
}
}
}
public static void main(String[] args) {
//从开始
result[0] = 1;
dfs(1, 4);
}
}
