堆的概念
堆首先是一个完全二叉树,我们先看一下完全二叉树的定义
若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
再看看堆的定义(二叉堆)
1.父节点的值总是大于(小于)或等于每一个子节点的值
2.每个结点的左子树和右子树也是一个堆
根据堆是一个二叉树,我们可以得出一些特性,假设当前结点在数组中的下标为i
- 一个结点的左儿子数据所在的下标为(i+1)*2-1
- 一个结点的右儿子数据所在的下标为(i+1)*2
- 一个结点的父结点数据所在的下标为(i-1)/2
对应可以写出一些代码:
public static int left(int i) {
return (i + 1) * 2 - 1;
}
public static int right(int i) {
return (i + 1) * 2;
}
public static int parent(int i) {
if (i == 0) { //下标为0的元素为根结点,不具有父结点
return -1;
}
return (i - 1) / 2;
}
根据堆是一个完全二叉树,可以得出一个特性,那就是从左往右看,最后一个父节点的索引下标为int i = parent(data.length - 1);
根据堆的特性可以得出,每个父结点都要大于等于它的子结点(大堆)或者每个根结点都要小于等于它的子节点(小堆),这样一来我们就知道根结点数据肯定是最大(小)的,我们可以利用这个特性进行排序,这就是所谓的堆排序,这个后面会提到。
如何建堆
先构建一组数据
int[] data = {1, 7, 3, 4, 9, 8, 3, 10, 2, 5};
将这组数据画成二叉树形式的图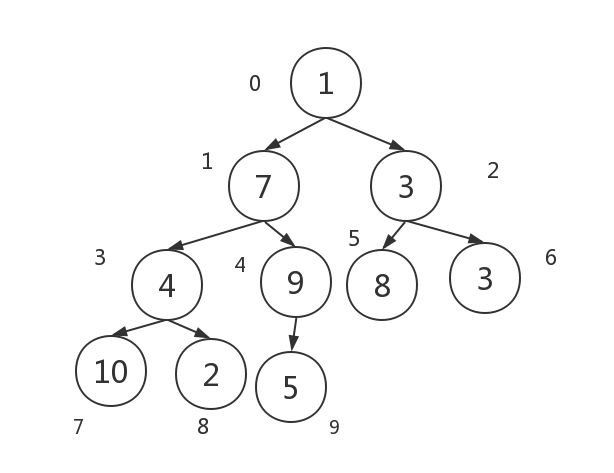
下面进行建堆(以大堆为例),根据上面的特性,我们需要做以下几步操作。
1.找到父节点跟其对应的子节点中最大的数,然后将其下标跟父结点交换
2.被交换的子节点可能导致原先建好的堆又不满足堆的特性,需要重写建堆
举个例子,我们看上图,从下标为4开始进行建堆,9和5两个数值满足堆的特点,不需要做处理,然后再看下标为3的子树,4,10,2三个数构成的树不满足堆的特点,将10和4交换位置,然后在看下标为1的子树,7,10,9三个数,将10和7换位置,此时需要注意的是7换到了原先建好的堆的根结点10,它的2个子节点原来是小于10的,但是不一定小于7,所以需要递归重新建堆一下。
3.对所有结点均进行建堆操作,可以根据上速特性过滤掉子节点。
下面贴出一次建堆的代码:
public static void maxHeapify(int[] data, int i) {//data是数据 i是结点所在下标
int l = left(i);
int r = right(i);
//先跟左右子结点比较,找出最大值
int largest = -1;
if (l < data.length && data[l] > data[i]) {
largest = l;
} else {
largest = i;
}
if (r < data.length && data[r] > data[largest]) {
largest = r;
}
if (i != largest) {
swap(data, i, largest);
maxHeapify(data, largest); //交换i和largest后,largest所在的结点对于的堆也需要再做以此最大堆处理
}
}
一次建堆完成后结果如图: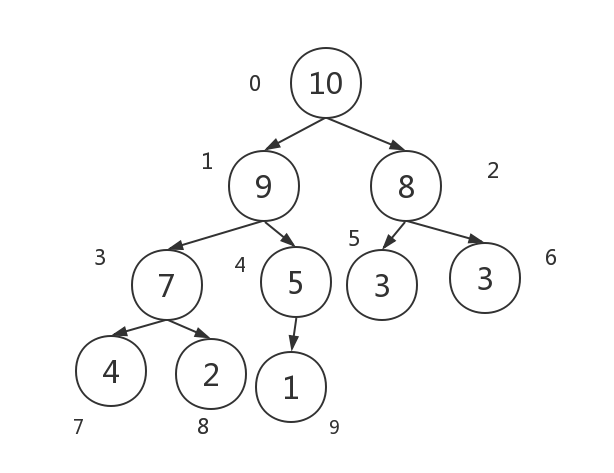
可以看到最大的数据在根结点,即下标为0的元素,此过程时间复杂度为logn.
对整个数据进行建堆操作:
public static void buildHeap(int[] data) {
//过滤掉右侧最后几个结点,此例中即下标为5,6,7,8,9的元素
int length = parent(data.length - 1);
for (int i = length; i >= 0; i--) {
maxHeapify(data, i);
}
}
如何进行堆排序
我们在前面已经知道了,构建一个堆(最大)的数据结构,可以得到这组数据中最大的元素。那么我们要想用它排序是不是每次取出第一个元素,然后将剩余元素重写建堆,再取第一个元素,再建堆,反复操作即可。实现代码如下:
int[] data = {1, 7, 3, 4, 9, 8, 3, 10, 2, 5};
int len = data.length;
int[] heapSort = new int[len];
for (int i = 0; i < len; i++) {
buildHeap(data);
heapSort[i] = data[0];
data = Arrays.copyOfRange(data, 1, data.length);
}
System.out.println(Arrays.toString(heapSort));
最后排序结果:[10, 9, 8, 7, 5, 4, 3, 3, 2, 1]
循环了n次,故整个堆排序时间复杂度为nlogn。如果要想从小到大排序,只需要建立小堆数据结构即可,就不多说了。
完整代码
/**
* ***堆***首先是一个***完全二叉树***,我们先看一下完全二叉树的定义
* >若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中
* 在最左边,这就是完全二叉树。
* 再看看堆的定义(二叉堆)
* >1.父节点的值总是大于(小于)或等于每一个子节点的值
* 2.每个结点的左子树和右子树也是一个堆
* Created by linuxv on 17-3-15.
*/
public class Heap {
public static void main(String[] args) {
int[] data = {1, 7, 3, 4, 9, 8, 3, 10, 2, 5};
int len = data.length;
int[] heapSort = new int[len];
for (int i = 0; i < len; i++) {
buildHeap(data);
heapSort[i] = data[0];
data = Arrays.copyOfRange(data, 1, data.length);
}
System.out.println(Arrays.toString(heapSort));
}
public static void buildHeap(int[] data) {
int length = parent(data.length - 1);
for (int i = length; i >= 0; i--) {
maxHeapify(data, i);
}
}
public static void maxHeapify(int[] data, int i) {
int l = left(i);
int r = right(i);
int largest = -1;
if (l < data.length && data[l] > data[i]) {
largest = l;
} else {
largest = i;
}
if (r < data.length && data[r] > data[largest]) {
largest = r;
}
if (i != largest) {
swap(data, i, largest);
maxHeapify(data, largest); //交换i和largest后,largest所在的结点对于的堆也需要再做以此最大堆处理
}
}
public static void swap(int[] data, int x, int y) {
int temp = data[x];
data[x] = data[y];
data[y] = temp;
}
public static int left(int i) {
return (i + 1) * 2 - 1;
}
public static int right(int i) {
return (i + 1) * 2;
}
public static int parent(int i) {
if (i == 0) {
return -1;
}
return (i - 1) / 2;
}
}